1inch revolutionizes automated market maker (AMM) segment with Mooniswap

The 1inch team is thrilled to release our cutting-edge automated market maker (AMM), Mooniswap, which redistributes earnings to liquidity pools, capitalizes on user slippages and protects traders from front-running attacks.

What is an AMM?

AMMs substantially change the way users swap cryptocurrencies. Liquidity pools allow users to easily switch between tokens in a fully decentralized and non-custodial way. Meanwhile, liquidity providers earn a passive income from trading fees that is based on the proportion of their contribution to the pool.

A bit of history

Bancor launched the first-ever AMM in 2017. This made it possible to trade cryptocurrency without relying on external data for pricing. Soon, innovative AMMs designed by different projects, such as Uniswap, Balancer, Curve, started springing up all over DeFi.

Alan Lu first used the constant-product invariant formula for prediction markets. Hayden Adams then used the beautiful formula for his AMM Uniswap. The elegant AMM formula reads:

x * y = k,

where

x — quantity of tokens x

y — quantity of tokens y

k — a fixed constant.

In other words, the equation expresses the dependency between quantities of two assets whose product has to remain constant. With this equation, an AMM is able to quote prices of two assets in a pool to sustain the product of their units equal to a constant.

The idea was taken up immediately. Vitalik Buterin called to “run on-chain decentralized exchanges the way we run prediction markets” and reflected upon the front-running problem. Indeed, the AMM mechanism imposes risks of losses on traders. These flaws have been addressed by many projects from different angles.

How does an AMM work?

The constant product invariant equation balances assets in a pool to always create two sides of a trade. The first side is traders who exchange with a pool causing the price skew. The latter side is arbitrageurs who come after the trades and by exchanging with a pool, bring the price back to market price. Thereby, we have two flows in and out of an AMM.

Traders are retailers who exchange assets at the price that an AMM offers them. They do not possess any specific information about the price condition at the market. Opposite goes for arbitrageurs. Often, they are bots that are designed to catch profitable deals. Arbitrageur flow is well-informed. Thus it has an upper hand over the rest of the market players.

Ideally, market makers would earn on that price divergence if the profit made on that price slippage goes back to the pool. Pools are pre-funded, therefore a swap can be executed with ease — without placing a bid and then waiting for a match. At any given period of time, one trader is selling while another is buying and in the end they offset each other.

Unfortunately, this does not play out in the real world. Traders that conduct front-running, literally steal from liquidity providers by trading on the price swings. The problem of front-running is undeniably important.

The problem with current AMMs

The constant product invariant formula formed the basis for many subsequent innovations around AMM design. DeFi has seen an explosion of AMMs that aim to improve the price curve.

The most direct implementation of the formula is Uniswap’s AMM. Uniswap is fully permissionless and can be funded by anyone. The Uniswap AMM works without any external feeds from oracles and basically has no other impacts on pricing apart from the trades executed against it. Unfortunately liquidity providers suffer losses when they withdraw in unfavorable conditions — impermanent losses. This is unpleasant.

With the creation of Curve giving better prices on stablecoins, Uniswap’s retail traders and liquidity providers started switching to more profitable sources. Curve developed a specific pricing function that consists of a constant product and constant sum. Thanks to the pool imbalance coefficient embedded in both sides of the equation, Curve’s AMM is able to quote prices more effectively. The AMM switches between constant sum and constant product formulas based on the extent to which the pool is imbalanced at the moment of query.

Curve’s innovation greatly contributes to the space but does not solve some of the most notorious problems.

As pioneers in the AMM space, Bancor first attempted to resolve high slippage on large trades and impermanent losses with liquidity amplification and dynamic weights mechanisms in their V2 update. But the floating weights solution for mitigating impermanent losses requires a smooth flow of price feeds from oracles that operate externally to the protocol. Bancor found this to be a critical drawback as oracles are vulnerable to front-running attacks. We align with Bancor’s view that a system is as strong as its weakest element.

Many projects have attempted to improve AMM design with their own unique implementations.

The 1inch team was most excited to design an AMM that enables liquidity providers to catch a portion of price slippage profits.

Introducing Mooniswap

Mooniswap is the next generation of an automated market maker with virtual balances — enabling liquidity providers to capture profits otherwise captured by arbitrageurs

Puzzled by the front-running problem, Vitalik Buterin proposed using “virtual quantities” but in a slightly different context.

The idea is fully realized in the Mooniswap design. The new AMM is capable of keeping most of the slippage revenue in the pool by maintaining virtual balances for different swap directions. When a swap happens, a market maker does not automatically apply the invariant algorithm and displays the new prices for upcoming trades. The AMM improves exchange rates for arbitrage traders slowly, over approximately a 5-minute time period. As a result, they will be able to collect only a portion of slippage, while the rest will remain in the pool shared among liquidity providers. This we believe is a game changer.

High competition among arbitrageurs would not allow them to wait for the point at which the price would maximize their profit. By such a delay in price updates, the market maker would create a highly competitive environment for arbitrageurs forcing them to perform trades at less profitable prices, which in turn would add value to the liquidity providers’ side.

The following chart shows how several arbitrages significantly increase constant product invariant from point X to point Q:

Slippy swap with 3 arbitrage trades

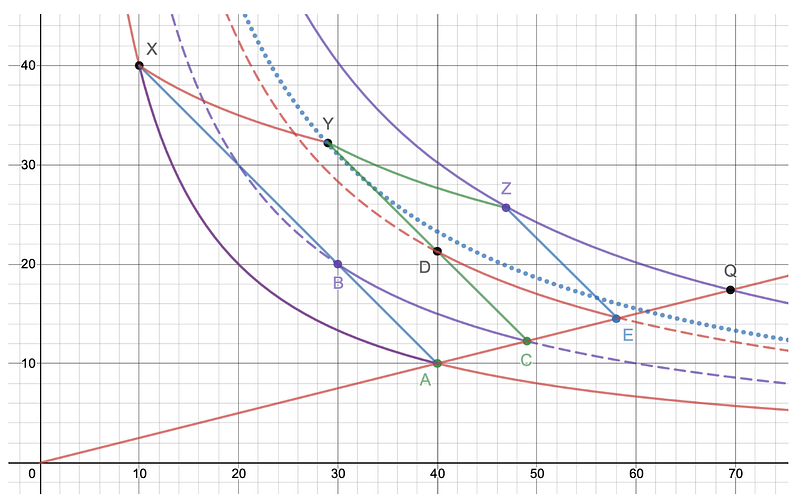
where

A — initial balances,

X — balances after a swap with the slippage,

B — virtual balances for the opposite swap after some period of time,

0A — 0Q — line where the price is real,

BC, DE, ZQ — arbitrage trades based on virtual balances,

XY, YZ — parallel transaction of arbitrage trades to real balances.

After the swap, virtual balances for the opposite swap started to move linearly from point A to point X, and at some point B, arbitrageurs found the price profitable and rebalanced the pool by performing the swap from point B to point C. Note that points A and C, as well as the origin, are all located on the same line — which means they have the same price. The chart shows three sequential arbitrage trades, which were performed until the real balance reached equilibrium price at point Q.

We have done multiple simulations of Mooniswap performance based on real world data and compared the results with Uniswap V2. Below, you can find the charts that display trading volume, cumulative price slippage, income of Uniswap V2 liquidity providers, along with the prediction of Mooniswap liquidity providers income. For illustration, we took some of the most liquid markets on Uniswap V2:

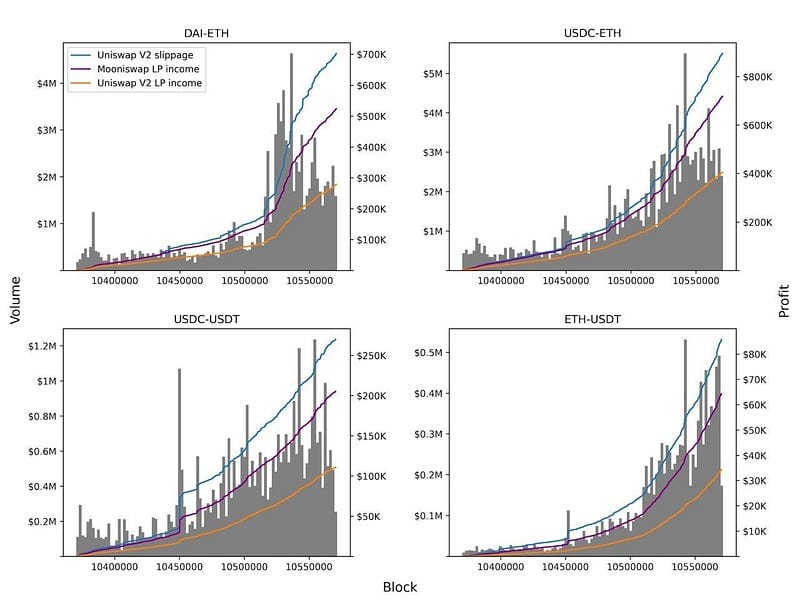
Comparison of Uniswap V2 LP income with potential Mooniswap LP income on different pools

On average we expect Mooniswap to generate from 50% to 200% more income for liquidity providers than Uniswap V2 due to redirection of price slippage profits.

Swap and Referral Fees

Mooniswap initially utilizes 0.3% Swap Fee which can be lowered all the way down to 0% in the future as a way to provide more competitive prices to the market.

Mooniswap introduces Referral Fee to incentivise integrations with wallets and other services that increase trading volume and additional income for liquidity providers. Referral Fee is only charged when the referral wallet is specified in transaction arguments.

Referral Fee is fixed and is equal to 5% of income earned by liquidity providers on the trade. So the initial 0.3% swap fee will be split to 0.015% going to referral and 0.285% going to liquidity providers. Additional profits generated by virtual balances are also split in the same ratio with 5% going to referral.

Referral Fee does not introduce additional pressure on the price and rewards external actors who contribute to the protocol by providing trading volume.

Apart from Swap Fee and Referral Fee, Mooniswap does not charge any additional protocol fees.

VWAP oracles

Mooniswap also introduces on-chain volume-weighted average price oracles. Price oracle data is stored as a cumulative sum of all trade inputs and outputs in both directions and it is updated after every transaction. By choosing different periods oracle users can configure the required level of price recency and manipulation resistance. We believe that due to Mooniswap’s utilization of virtual balances, VWAP oracles will be hard to manipulate by malicious actors.

The Mooniswap user interface is indebted to Uniswap. Uniswap interface has proven to be intuitive, reliable and loved by many users.

The mooni is looking forward to your arrival!

Mooniswap exchange https://mooniswap.exchange/

Twitter https://twitter.com/mooniswap

Telegram Channel: https://t.me/mooniswap

Telegram Chat: https://t.me/mooniswapchat

Discord https://discord.com/invite/FZADkCZ